
Un jour sur ses longs pieds allait je ne sais où
L'échassier au long bec, emmanché d'un long cou ;
Il côtoyait une avocette...
– Qui êtes vous ? lui dit-elle.
– Je suis le roi du triangle d'argent ; on me nomme Ptolémée.
– Décrivez moi votre royaume.
– Il se trouve en Vendée, au Pays des Olonnes, à quelques kilomètres au nord de la plus belle plage d'Europe ; son nom lui vient des marais salants qu'un vieux paludier entretient avec amour.
– Mais encore ?
– C'est un triangle dont les côtés ont des mesures qui, exprimées en mètres, sont trois nombres entiers consécutifs ; et son aire, exprimée en centiares, est aussi un nombre entier.
– Est ce grand ?
– Oui et non : mon royaume est plus petit que celui de mon grand-père qui atteignait les quarante kilomètres carrés ; mais il est plus grand que celui de mon jeune frère qui ne mesure que trente hectares.
– Ah ! Et quel est son périmètre ?
– Ca, c'est à vous de me le dire...
Quel est, en mètres, le périmètre du royaume de Ptolémée ?
Deux indices (une parodie de « Le Héron, la Fille », 1678, fable de La Fontaine ; et Ptolémée, nom des souverains grecs qui régnèrent sur l’Egypte après la mort d’Alexandre en 323 avant J.-C.) devaient orienter le lecteur vers l’utilisation d’une formule que l’on attribue à Héron d’Alexandrie et qui permet le calcul de l’aire d’un triangle

Soient a = N - 1, b = N et c = N + 1 les mesures des côtés du triangle d’argent (le royaume de Ptolémée)
2.p = (N - 1) + N + (N + 1) et donc 2.p = 3.N,
d’où p - a = (N + 2) / 2
p - b = N / 2
p - c = (N - 2) / 2
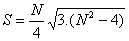
N est nécessairement pair (sinon S ne serait pas entier) ;
posons donc N = 2.x
on a donc
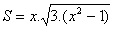
Calculatrice et/ou ordinateur permettent assez vite de trouver les premiers termes de la suite des x tels que 3.(x²-1) est un carré (condition nécessaire et suffisante pour que S soit entier) ; ce sont
1 ; 2 ; 7 ; 26 ; 97 ; 362 ; 1351 ; 5042 ...
d’où les valeurs de N et de S correspondantes :
| N : | 2 | 4 | 14 | 52 | 194 | 724 | 2 702 | 10 084 |
| S : | 0 | 6 | 84 | 1 170 | 16 296 | 226 974 | 3 161 340 | 44 031 786 |
Dans le tableau ci-dessus, les valeurs de N sont exprimées en mètres ; celles de S en mètres carrés, c’est à dire en centiares.
30 ha = 300 000 ca
40 km² = 40 000 000 ca
La seule possibilité est donc 3 161 340 ca (sinon le royaume de Ptolémée serait ou plus grand que celui de son grand-père, ou plus petit que celui de son jeune frère).
On a donc N = 2 702 m ; d’où le périmètre cherché : 2.p = 8 106 m.
Le périmètre du royaume de Ptolémée est de 8 106 mètres.
Voici quelques compléments pour les plus curieux :
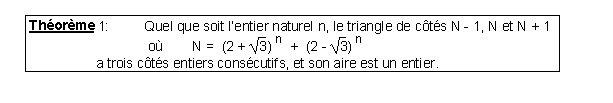
la démonstration, assez simple, s’effectue en trois temps :
on montre d’abord que le nombre ci-dessous est entier :
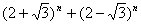
puis que :
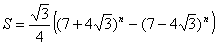
et enfin que ce nombre est entier.
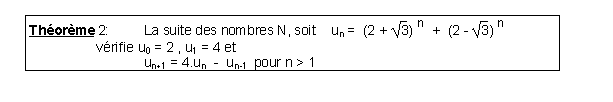

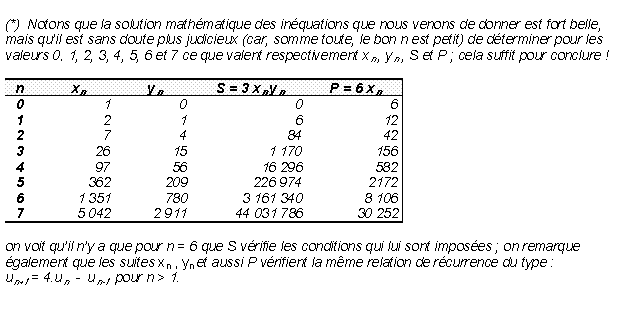
la démonstration de ces résultats est laissée en guise d’exercice au lecteur ; il est à noter que les formules de récurrence contenues dans ces théorèmes lui permettront de recalculer par lui-même les valeurs de N et de S inscrites dans le tableau présenté plus haut.
Voici enfin un peu de calcul mathématique pour l’amour de l’art...
En fait, l’équation à résoudre dans ce problème, à savoir
3.(x² - 1) = k²
où x est la moitié de N , côté médian de notre triangle, est une équation diophantienne, c’est à dire une équation aux coefficients et inconnues entiers.
Notons que Diophante, tout comme Héron, était un mathématicien d’Alexandrie.
Mais, revenons à notre équation ; k² étant multiple de 3, posons alors k = 3 y ; l’équation s’écrit maintenant :
3.(x² - 1) = 9 y²
ou encore
x² - 3 y² = 1
Il s’agit d’une équation diophantienne particulière, dite de Pell-Fermat, dont les solutions sont les couples (xn ; yn) tels que
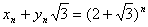
L’aire S du triangle étant telle que
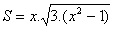
on a S = 3 x.y
Il convient maintenant de trouver pour quelle(s) valeur(s) de n on aura la double inégalité suivante vérifiée :
300 000 < 3 xn yn < 40 000 000
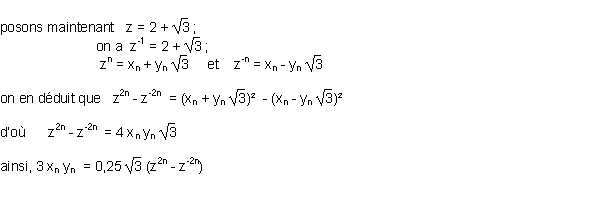


Ce problème a été posé durant tout le mois d'octobre 2000, dans le cadre d'un concours organisé par Q.I. à l'occasion de la Fête de la Science, afin de "marquer le coup" en 2000, année mondiale des MATHEMATIQUES.
Quadrature Infernale a reçu un certain nombre de réponses à son concours ; la plupart étaient bonnes et accompagnées de solutions intéressantes ; les moyens utilisés furent variés : mathématiques pures assez rarement ; mathématiques et informatique le plus souvent (langage C ou Fortran ou CamL ; Excel ou calculatrice)...
Parmi les bonnes réponses, notons :
en Sarthe
Florent CALVAYRAC, Le Mans, UFR Sciences (LPEC) ; Meilleur sarthois (ex aequo)
Patrick DONNET, Le Mans, IUT (Directeur)
Catherine GALOPIN et Juliette CONSTANT, Le Mans ; Meilleurs sarthois (ex aequo)
Yves OLLIVIER, Le Mans, IUT (GEA) ; Meilleur sarthois (ex aequo)
Mickael PARIS, Le Mans, UFR Sciences ; Meilleur Etudiant de l'Université du Maine(LRM)
Denis ROQUET, Le Mans, IUT (GMP) ; Champion des Pays de la Loire
Alain WROBEL, Le Mans, UFR Lettres (GREGUM-UMR ESO)
en Mayenne
Sophie DORNIC, Beaumont Pied de Boeuf ; Meilleur mayennais (ex aequo)
Ophélie et Laurence GEMOND, Laval ; Meilleurs mayennais (ex aequo)
Ailleurs, et donc hors concours :
Daniel COLLIGNON, Chatenay-Malabry, INSEE
Emmanuel HAINRY, Lyon, ENS
Alain François HEUDE, Université Perpignan (F)
Les étudiants en DEA Gestion/Finance de Mons (B), FUCAM
Yann LONGIN, Lille, Communauté Urbaine
Michel TANGUY, Quimper
Bravo à tous ceux qui ont cherché (qu'ils aient envoyé ou pas une réponse)
Félicitations à ceux qui ont trouvé !
Ses parrains sont : ROTARY-CLUB de LAVAL ; VILLE de LAVAL ; DEPARTEMENT de la MAYENNE ; UNIVERSITE du MAINE ; CREDIT AGRICOLE ; BIJOUTERIE A. BOURDAIS