

Cloche, Couronne, Ecu, Cavalier, Raisin, Jésus, Colombier, Univers…
La réponse est simple et tous les cyberlecteurs - en particulier ceux qui lisent aussi livres et cahiers - sont concernés puisqu ‘il s’agit de formats de papier ; des formats associés aux dimensions d’une feuille de papier : ainsi le format “cloche” correspond à une largeur de 30 cm et une longueur de 40 cm; le “raisin” à 50 cm x 65 cm. le “jésus” à 56 cm x 76 cm; l’“univers” à 100 cm x 130 cm …
Une feuille de papier est généralement destinée à être pliée (voire coupée) en deux, quatre, huit, seize pour donner les pages d’un même livre ou journal. Ainsi, un in-quarto -ce qui veut dire “en quatre”- est une feuille qui a subi deux plis pour donner 4 feuillets (2x2), soit 8 pages. Les pages d’un in-quarto jésus mesurent 28 cm x 38 cm : celles d’un in-seize jésus 14 cm x 19 cm (elles ont été pliées 4 fois, ce qui donne 16 feuillets -2x2x2x2-, donc 32 pages)…
Les formats cités plus haut, pour la plupart très anciens, ont deux inconvénients majeurs :
La surface d’une feuille de papier est un nombre compliqué ;
Les proportions de la feuille (rapport longueur / largeur) ne sont pas conservées lorsque celle-ci est pliée ou coupée en deux (deux parties égales).
Afin de remédier à ces inconvénients, on a cherché - et trouvé - un format tel que la surface d’une feuille soit 1 mètre carré et que ses proportions soient conservées lors d’un pliage le long de la plus petite de ses médianes.
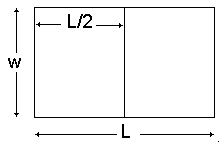
Reprenons les hypothèses :
la feuille a une longueur L (en mètres)
et une largeur w (en mètres)
telles que L . w = 1 (surface en mètres carrés)
la demi-feuille a pour longueur w
et pour largeur L / 2
bien sûr sa surface est 1 /2 mètre carré.
surtout, on veut L / w = w / (L / 2)
On en tire, en posant L / w = x, l’équation x = 2/x,
soit x ^ 2 = 2.;
Le nombre x = L / w est l’unique nombre positif dont le carré vaut 2 ; on l’appelle la racine carrée de 2.
On écrit L / w = 2 ^ (1/2).
Une calculatrice montre que 2 ^ (1/2) = 1,414…
Il vient x = 2 ^ (1/2), soit L = w . 2 ^ (1/2).
En remplaçant w par 1/L, on trouve que
L ^ 2 = 2 ^ (1/2) c’est à dire L ^ 4 = 2.
Le nombre positif qui vérifie cette équation est unique et s’appelle la racine quatrième de 2.
On écrit L = 2 ^ (1/4) ou encore L = (2 ^ (1/2)) ^ (1/2)
Une calculatrice en donne la valeur approchée L = 1,189… et pour son inverse w = 0,841…

La feuille de 1 mètre carré de format normalisé international (dont on vient de calculer les longueur et largeur) est représentée par le symbole A0, la demi-feuille par A1, le quart de feuille par A2 dans le tableau ci-dessous (valeurs approchées)
| Format | Longueur (en mm) | Largeur (en mm) | Surface (en mm²) | L/w |
|---|---|---|---|---|
| A0 | 1189 | 841 | 1000000 | 1,414 |
| A1 | 841 | 595 | 500000 | 1,414 |
| A2 | 595 | 420 | 250000 | 1,414 |
| A3 | 420 | 297 | 12500 | 1,414 |
| A4 | 297 | 210 | 62500 | 1,414 |
| A5 | 210 | 148 | 31250 | 1,414 |
On retrouve bien sûr le très fameux format A4 (21 cm x 29,7 cm) et on vérifie que L/w ne change pas : c’est un invariant de la série normalisée. Nous avons vu plus haut que L/w = 2 ^ (1/2).
Une feuille de 1 mètre carré pèse 80 g. Une enveloppe et son timbre pèsent 3g . Combien de feuilles de format A4 peut-on mettre dans l’enveloppe
si celle-ci est timbrée à 3,00F ? (maximum 20g)
si elle est timbrée à 4,50F ? (maximum 50g)
Combien faut-il de feuilles de format Ao pour réaliser un livre de 192 pages de format A5 ?
Déterminer la longueur et la largeur d’une feuille de format A10.
On montre d’abord qu’une feuille de format A4 pèse 5 g ;
alors, on trouve :
pour a) 3 feuilles
pour b) 9 feuilles.
Il y a 2 ^ 5 = 32 feuilles A5, soit 64 pages dans une feuille A0 ;
il en faut donc 3.
Le lecteur trouvera tout seul ; s’il réussit, ce dont nous ne doutons pas, il pourra vérifier que longueur + largeur = 63 mm.