Introduction

Mars 2005,

Le problème ci-dessous a été posé par André LEBLE, Professeur de physique au département “mesures physiques” de l’I.U.T. du Mans ; la deuxième démonstration lui doit beaucoup.

Enoncé du problème (parallèles dans un triangle)

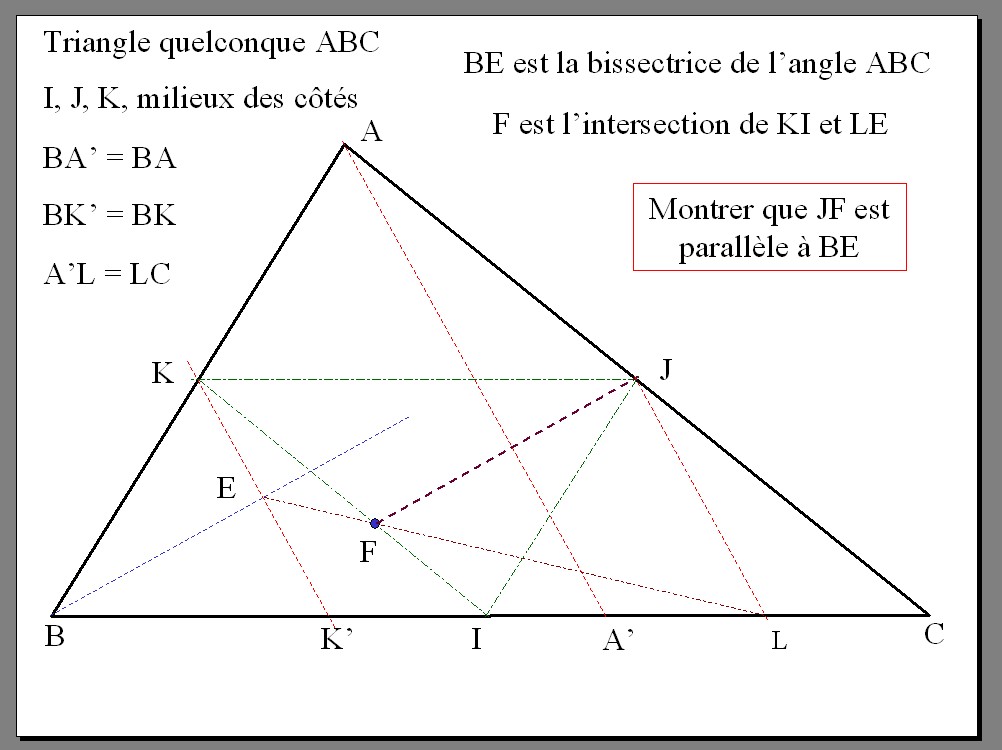
Soit un triangle quelconque ABC ; on note I, J, K les milieux des côtés [BC], [CA], [AB] ;

A’ est le point de BC tel que BA’ = BA ; K’ est le point de BC tel que BK’ = BK ;

L est le milieu de [A’C] ; E est le point commun à (KK’) et à la bissectrice de l’angle ABC ;

F est le point d’intersection de (KI) et de (LE).

→ On demande de montrer que (JF) // (BE)

Un petit dessin et tout devient clair !

Voici une première démonstration (analytique)

Choisissons ainsi les coordonnées de B, A’, et C : B (0 ; 0) ; A’ (4a ; 0) ; C (4c ; 0)

et notons b l’angle ABC

bien sûr, a + c ≠ 0 et asin b ≠ 0 sauf si le triangle (ABC) est plat, cas dans lequel le résultat cherché est évident.

On a :

K’ (2a ; 0) ; I (2c ; 0) ; L (2a+2c ; 0) ; K (2acosb ; 2asinb) ;

E (a(1+cosb) ; asinb) ; A (4acosb ; 4asinb) ; J (2c+2acosb ; 2asinb)

On en déduit que :

(KI) : x = 2c + y.((acosb-c)/asinb) et

(LE) : x = 2a+2c + y.((a(cosb-1)-2c)/asinb)

D’où :

F ((2a²cosb+2c²)/(a+c) ; (2a²sinb)/(a+c))

Ce qui permet de montrer que :

Vect(JF) = [-2c/(a+c)].Vect(BE)

D’où le résultat :

(JF) // (BE)

qed ; G.H.

Remarque : si on note Z le point d’intersection de (JF) et de (BC), on a Z (2c-2a ; 0)

ce qui montre que I est milieu de [ZL] et que BZ = LC.

Voici une seconde démonstration (géométrique)

Posons a = BC ; b = CA ; c = AB . Notons G le barycentre de [ I (a) ; J (b) ; K (c) ]

puis i l’angle KIJ et k l’angle IKJ

bien sûr, a , b , et c n’ont rien à voir avec ceux de la précédente démonstration

On a : G = bary { [ I (a) ; J (b) ; K (c) ] }

= bary { [ K’ (c) ; L (a-c) ; J (b) ; K (c) ] }

= bary { [ E (2c) ; L (a-c) ; J (b) ] }

Donc

G = bary { [ F (a+c) ; J (b) ] }

où F = bary { [ E (2c) ; L (a-c) ] } = bary { [ I (a) ; K (c) ] }

( et F est point d’intersection de (EL) et de (IK) )

On a ainsi :

a.FI = c.FK

d’où [a/sin(i)].d[F;(IJ)] = [c/sin(k)].d[F;(KJ)]

mais [a/sin(i)] = 2. KJ/sin(i) = 2. IJ/sin(k) =[c/sin(k)]

d’où d[F;(IJ)] = d[F;(KJ)]

On en déduit que (JF) est la bissectrice de l’angle KJI

comme (BE) est la bissectrice de l’angle ABC et puisque (BKJI) est un parallélogramme ¹

on peut conclure que :

(JF) // (BE) ²

qed ; A.L. et G.H.

Remarque :

Ce problème est issu de la recherche du centre de gravité d’un tri-tige ABC, qui contrairement à un triangle “ordinaire” n’est pas le point de rencontre des médianes, mais le point d’intersection des bissectrices du triangle formé par les milieux des côtés.